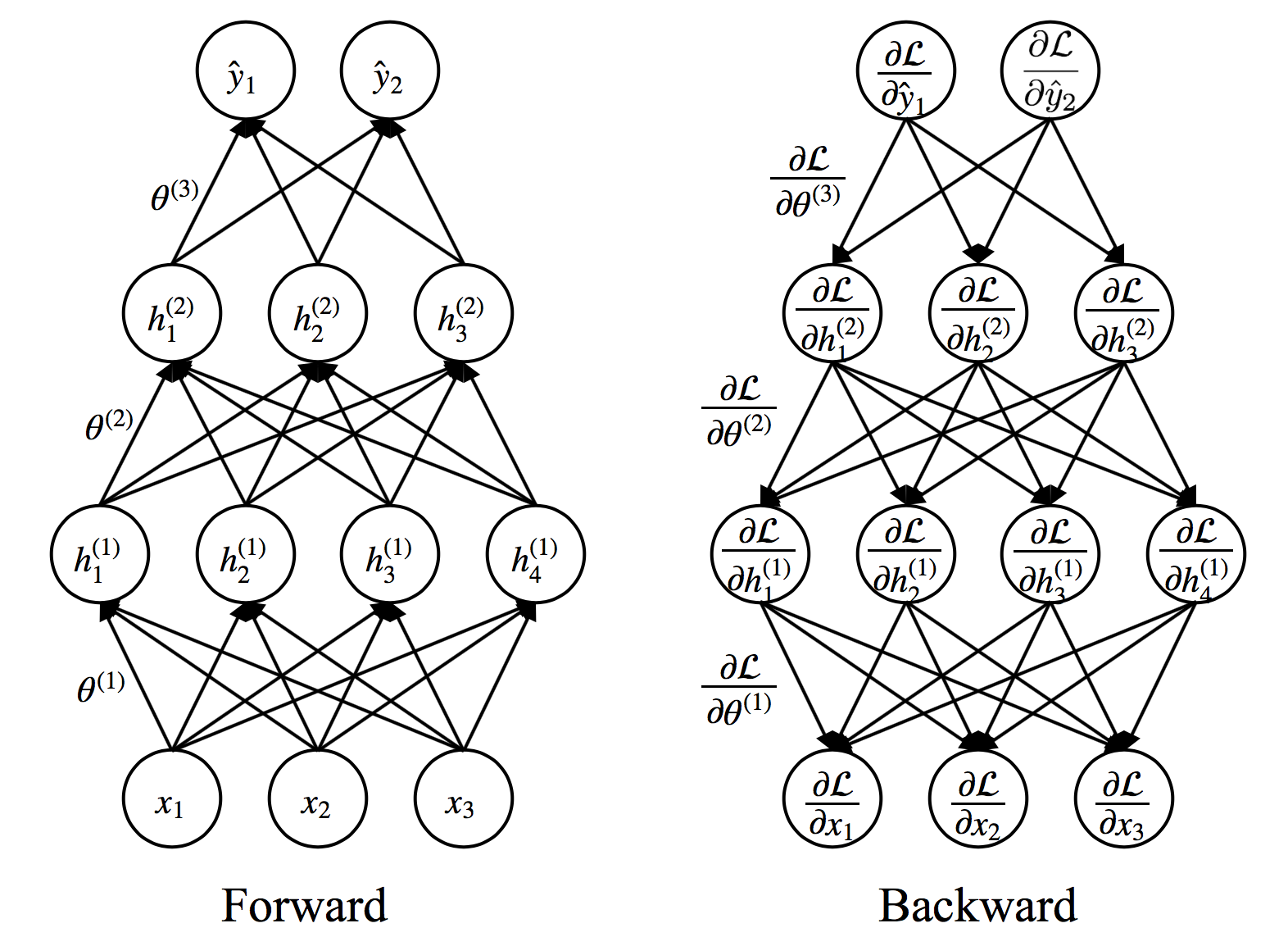
Training Neural Networks¶
Repeat until convergence
- $(\textbf{x},\textbf{y}) \leftarrow$ Sample an example (or a mini-batch) from data
- $\hat{\textbf{y}} \leftarrow f\left( \textbf{x} ; \theta \right)$ Forward propagation
- Compute $\mathcal{L}\left(\textbf{y},\hat{\textbf{y}}\right)$
- $\nabla_{\theta}\mathcal{L} \leftarrow$ Backward propagation
- Update weights using (stochastic) gradient descent
- $\theta \leftarrow \theta - \alpha \nabla_{\theta}\mathcal{L}$
Types of Losses: Squared Loss¶
$$ \mathcal{L}\left(\textbf{y},\hat{\textbf{y}}\right) = \frac{1}{2}\left\Vert \textbf{y}-\hat{\textbf{y}}\right\Vert^2_2 $$$$ \frac{\partial\mathcal{L}}{\partial \hat{y}_i}=\hat{y}_i-y_i \iff \nabla_{\hat{\textbf{y}}}\mathcal{L}=\hat{\textbf{y}}-\textbf{y} $$- Used for regression problems
Newton's Method: Overview¶
- Goal: Minimize a general function $F(w)$ in one dimension by solving for $$ f(w) = \frac{\partial F}{\partial w} = 0 $$
- Newton's Method: To find roots of $f$, Repeat until convergence: $$ w \leftarrow w - \frac{f(w)}{f'(w)} $$
Geometric Intuition¶
- Find the roots of $f(w)$ by following its tangent lines. The tangent line to $f$ at $w_{k-1}$ has equation $$ \ell(w) = f(w_{k-1}) + (w-w_{k-1}) f'(w_{k-1}) $$
- Set next iterate $w$ to be root of tangent line: $$ \begin{gather} f(w_{k-1}) + (w-w_{k-1}) f'(w_{k-1}) = 0 \\ \implies \boxed{ w = w_{k-1} - \frac{f(w_{k-1})}{f'(w_{k-1})} } \end{gather} $$
Application to minimization¶
To minimize $F(w)$, find roots of $F'(w)$ via Newton's Method.
Repeat until convergence: $$ \boxed{w \leftarrow w - \frac{F'(w)}{F''(w)}} $$
Minimization in multivariate case¶
Replace second derivative with the Hessian Matrix, $$ H_{ij}(w) = \frac{\partial^2 F}{\partial w_i \partial w_j} $$
Newton update becomes: $$ \boxed{ w \leftarrow w - H^{-1} \nabla_w F} $$
- Advantage: Fast convergence (quadratic)
- Disadvantage: Computing Hessian and its inverse is slow
Sometimes line search is necessary¶
Let $p=-H^{-1} \nabla_w F$, find a step size $\alpha$ such that $$ \min_\alpha F(w+\alpha p) $$ Then $$ \boxed{ w \leftarrow w - \alpha H^{-1} \nabla_w F} $$
Issues¶
- Computing Hessian is expensive
- Approximate linear solve for $H^{-1}$
- Quasi-Newton methods: Construct approximate $H$ from past gradients (e.g. BFGS using secant equation) $$\mbox{Scalar:}\quad F''(w_{k+1}) \approx [F'(w_{k+1}) - F'(w_k)]/(w_{k+1}-w_k)$$ $$\mbox{Vector:}\quad H_{k+1}(w_{k+1}-w_k) \approx \nabla_w F(w_{k+1}) - \nabla_w F(w_k)$$
- Do not work well for non-convex problems
- It only solves for $\nabla_w F=0$
- The solution can be a saddle point, or even a maximizer!
- Possible to use the Levenberg-Marquardt algorithm (regularizing the Hessian) $$\tilde{H} = \lambda I + H,\quad \lambda>0$$
Unfortunately, saddle points prevail in high dimensions¶
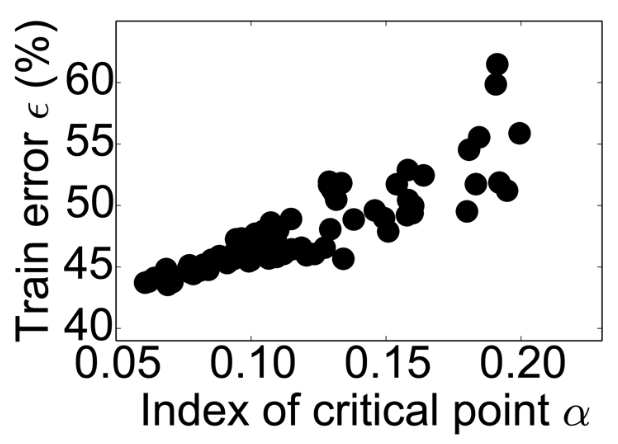
The $\epsilon-\alpha$ curve [1]
- $\alpha$: Percentage of negative eigenvalues of Hessian at critical point (i.e. gradient=0)
- $\epsilon$: Error at critical point
- There are many saddle points (the figure is for a relatively small NN)
- Strong positive correlation between $\alpha$ and $\epsilon$, esp. in high-dim optimization
[1] Y. Dauphin et al. Identifying and attacking the saddle point problem in high-dimensional non-convex optimization. NeurIPS 2014.
Intuitively, in high dimensions, the chance that all the directions around a critical point lead upward (positive curvature) is exponentially small w.r.t. the number of dimensions
Implications:
- If you get a "converged" model and it does not perform well, then the model is likely at a saddle point
- The local minima are likely to be as good as global minima
- For even larger problems, even saddle points with low index are sufficient (which is more common)
- Now that Hessian-based method might be problematic, we should just use Gradient Descent
Simple Gradient Descent¶
Batch mode¶
Given dataset $\{ (x,t) \}$ and initial guess $\vec{w}_0$, repeat until convergence:
- $\vec{w} = \vec{w} - \eta \nabla_\vec{w} E(\vec{w})$
where $\eta$ is the step size(s), or learning rate, and assuming quadratic loss,
$$ \nabla_w E(\vec{w}) = \sum_{n=1}^N \left[ f\left( \textbf{x}^{(n)} ; \theta \right) - y^{(n)} \right] \frac{\partial f\left( \textbf{x}^{(n)} ; \theta \right)}{\partial \theta} $$- Disadvantage: Can be slow if the network is large and the dataset is huge
Stochastic mode, a.k.a., Stochastic Gradient Descent (SGD)¶
Main Idea: Instead of computing batch gradient (over entire training data), just compute gradient for individual example and update.
Repeat until convergence: for $n=1,\dots,N$
$$ w := w - \eta \nabla_\vec{w} E(\vec{w} | \vec{x}^{(n)}) $$where
$$ \nabla_w E(\vec{w} | \vec{x}^{(n)}) = \left[ f\left( \textbf{x}^{(n)} ; \theta \right) - y^{(n)} \right] \frac{\partial f\left( \textbf{x}^{(n)} ; \theta \right)}{\partial \theta} $$- Advantage: Easier to compute, esp. when the dataset is huge; sometimes can escape local minima
- Disadvantage: The gradient becomes noisy - impacts convergence; the Hessian is not well-defined even if we want to use it
- In between there are "mini-batch" mode
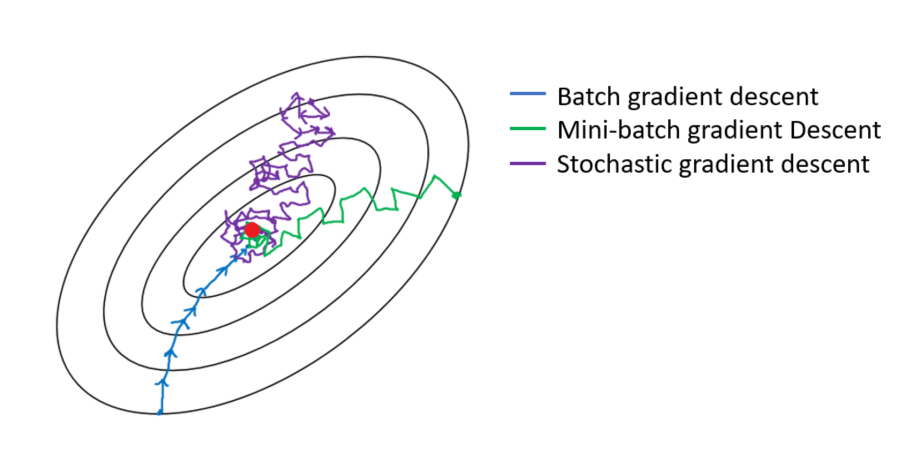
Comparison - Batch mode seems more reliable?¶
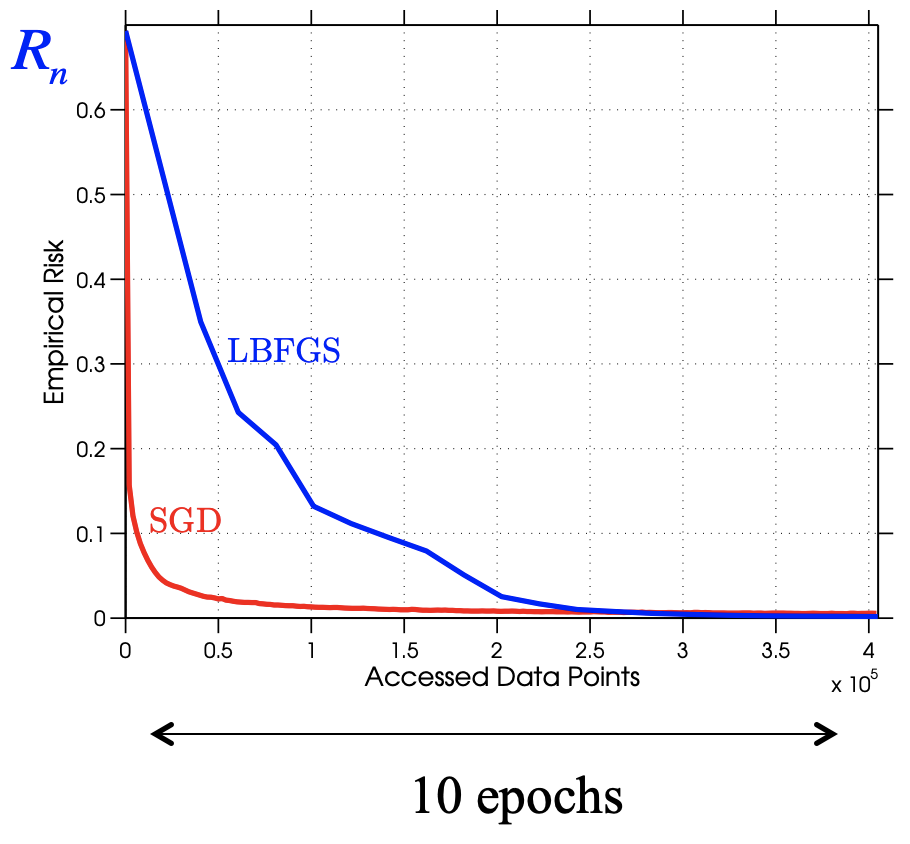
Comparison - but if we look at cost¶
- Think LBFGS as batch GD
- SGD shows fast initial progress, though slowed down later.
Let $n$ be the batch size, $\epsilon\sim 10^{-3}$ the final "loss", $T$ the allowable time, then [1]
- Batch: Work$\sim n\log(1/\epsilon)$, Error$\sim(\log(T)+1)/T$ - better to focus on a certain number of samples
- Stochastic: Work$\sim 1/\epsilon$, Error$\sim 1/T$ - just process as many samples as possible
[1] L. Bottou, et al. Stochastic Gradient Methods For Large-Scale Machine Learning. Arxiv: 1606.04838; Also here as slides: http://users.iems.northwestern.edu/~nocedal/ICML
Practical SGD methods¶
$$ w := w - \eta \nabla_\vec{w} E(\vec{w} | \vec{x}^{(n)}) $$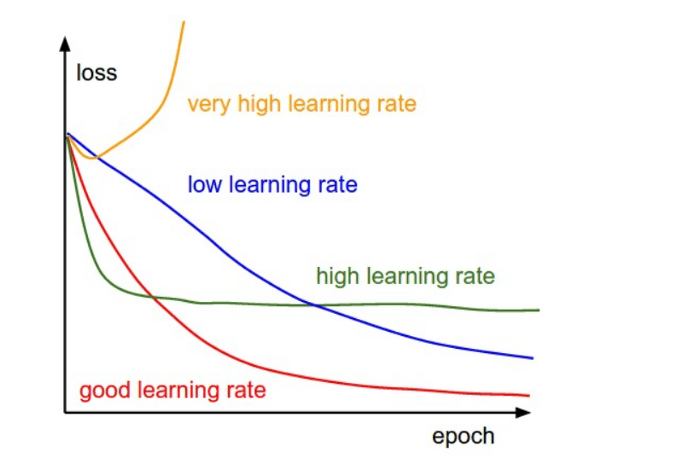
- How to determine learning rate?
- How to improve convergence rate?
- Getting out of saddle points?
Fancier variants¶

SGD with momentum¶
Let the optimizer remember the previous gradients, $$ v_k = \rho v_{k-1} + (1-\rho)\nabla_w F(w_k) $$ Then $$ \boxed{ w_{k+1} = w_k - \eta v_k} $$
- Momentum is a weighted sum of gradients, weights for old gradients decay exponentially
- Less sensitive to noise
- Easier to pass local minimum
AdaGrad¶
Let the optimizer tune learning rate automatically, $$ g_k = g_{k-1} + [\nabla_w F(w_k)]^2 $$ Then $$ \boxed{ w_{k+1} = w_k - \frac{\eta}{\sqrt{g_k}+\epsilon} \nabla_w F(w_k)} $$
- Note that the square and sqrt are element-wise, $\epsilon\sim 10^{-6}$ to avoid division by zero
- Learning rate decreases as the solution moves longer distance
- Now $\eta$ can be very large - It will become small anyways
RMSProp¶
Similar to AdaGrad, but allow the optimizer to "forget", $$ g_k = \alpha g_{k-1} + (1-\alpha)[\nabla_w F(w_k)]^2 $$ Then $$ \boxed{ w_{k+1} = w_k - \frac{\eta}{\sqrt{g_k}+\epsilon} \nabla_w F(w_k)} $$
- Like momentum, let old squared gradient decay exponentially. Typically $\alpha=0.9$.
- The rest is AdaGrad.
Adam¶
Combine the best of SGD w/ momentum and RMSProp, $$v_k = \beta_1 v_{k-1} + (1-\beta_1)\nabla_w F(w_k)$$ $$g_k = \beta_2 g_{k-1} + (1-\beta_2)[\nabla_w F(w_k)]^2$$ Then $$ \boxed{ w_{k+1} = w_k - \frac{\eta}{\sqrt{g_k}+\epsilon} v_k} $$
- Sometimes $v_k$ and $g_k$ are corrected before updating $w$, $$ v_k \leftarrow \frac{v_k}{1-\beta_1^k},\quad g_k \leftarrow \frac{g_k}{1-\beta_2^k} $$
- It was suggested to use $\beta_1=0.9$, $\beta_2=0.999$.
More methods¶
People have devised many, many other gradient-descent methods. Some perform the best in some specific applications, but there is not "one-for-all" solution.
You will implement one of them in HW3.
There are also attempts to combine the advantages of different methods, e.g. [1]
[1] N. Keskar, R. Socher, Improving Generalization Performance by Switching from Adam to SGD, Arxiv 1712.07628
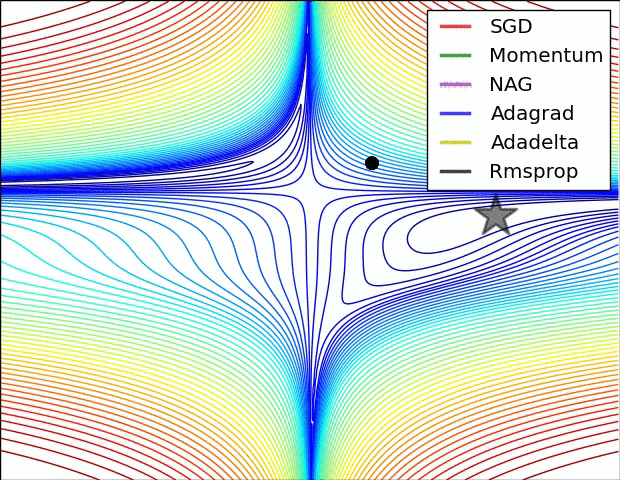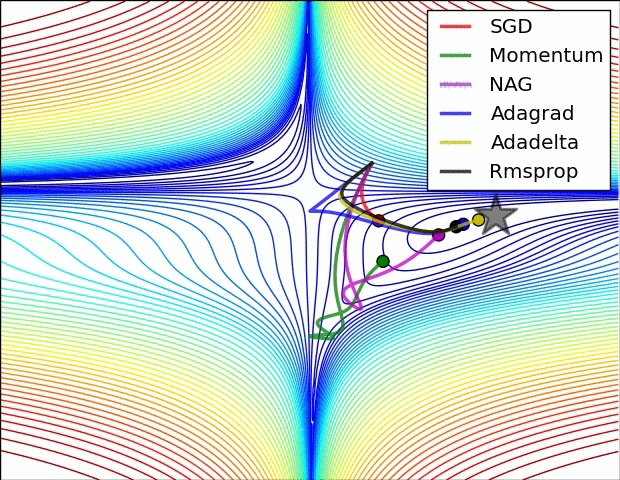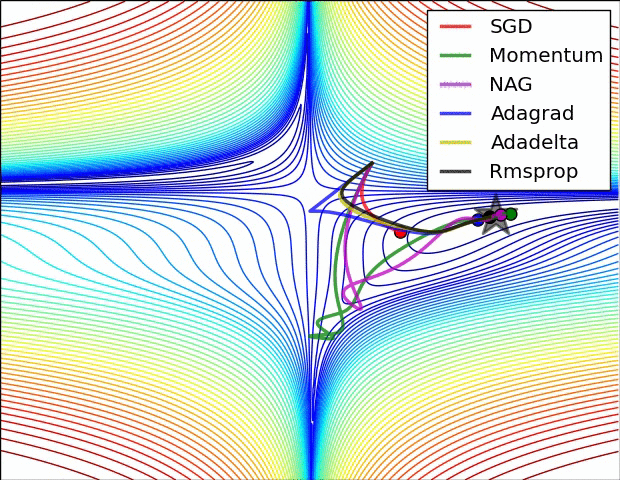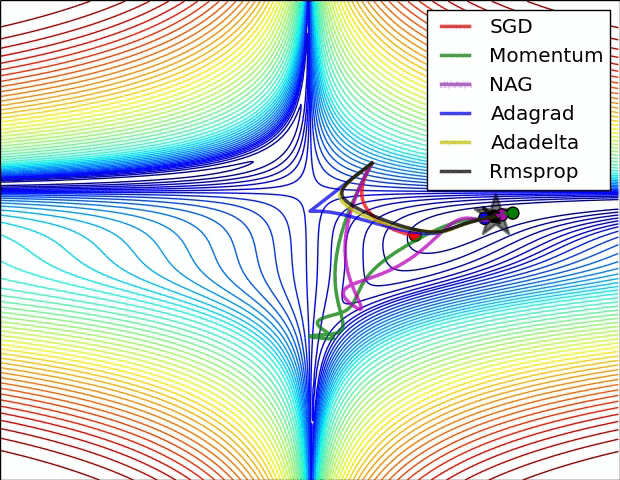
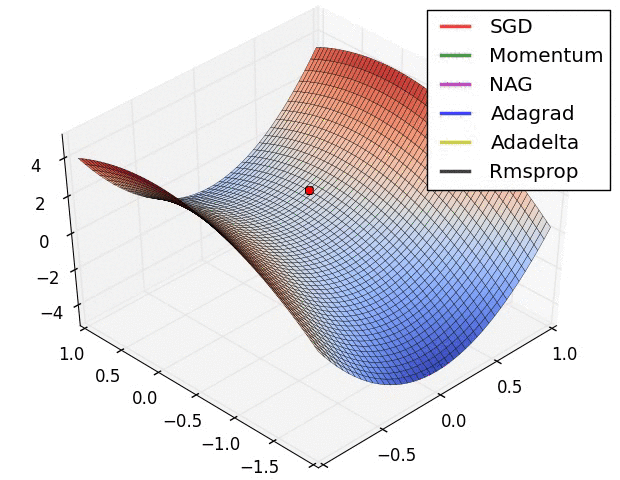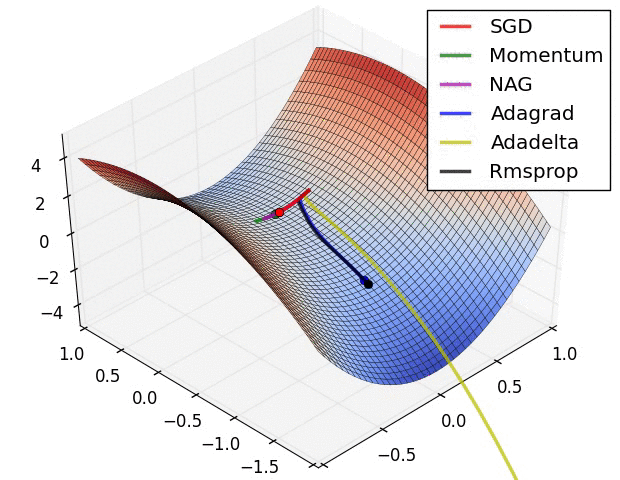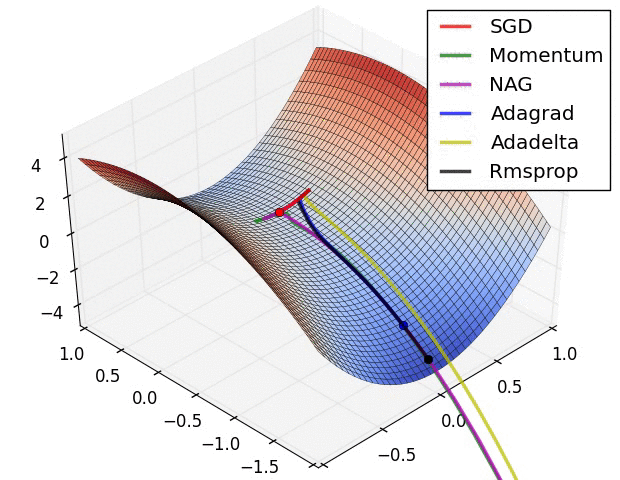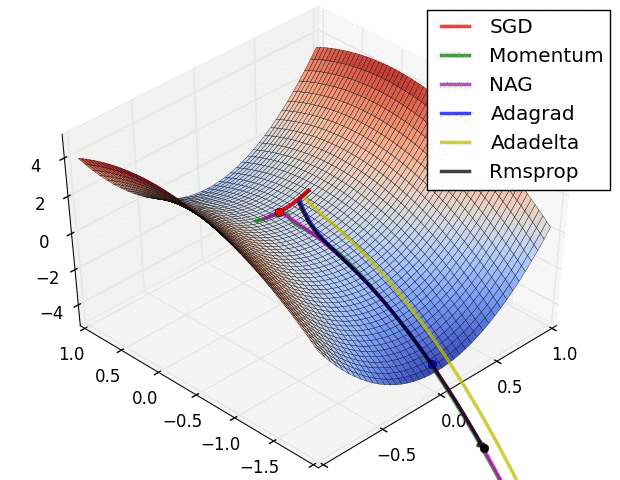
x0 = [-1.5,0.5]
# x0 = [1.0, 0.0]
# xs, fs, gs, hs = gradDesc(FGH, x0, BBLR)
# xs, fs, gs, hs = gradDesc(FGH, x0, BFGS, ifLS=True)
# xs, fs, gs, hs = gradDesc(FGH, x0, NR, ifLS=True)
x0 = [-1.5,0.5]
ss = 0.5 # Noise in gradient
# xs, fs, gs, hs = gradDesc(FGHS(ss), x0, fixLR(0.0001))
# xs, fs, gs, hs = gradDesc(FGHS(ss), x0, GDM(0.0001,0.9))
# xs, fs, gs, hs = gradDesc(FGHS(ss), x0, AdaGrad(2.0))
# xs, fs, gs, hs = gradDesc(FGHS(ss), x0, RMSProp(0.1,0.9))
xs, fs, gs, hs = gradDesc(FGHS(ss), x0, Adam(0.1,0.9,0.999))
f1, ax = pltFunc()
ax[0] = pltTraj(ax[0], xs)
ax[1] = pltHist(ax[1], xs)
One more awesome interactive visualization: https://github.com/lilipads/gradient_descent_viz
Now that we know there are many saddle points and local minima...¶
- What kind of local minima is better? The flat ones - (empirically) better generalization performance
- Compare Adam and vanilla SGD [1]
- Adam escapes saddle point easier (see the GIF earlier)
- SGD favors flat minima more
Additional conclusion from [1]: A small learning rate or large-batch makes it much harder to escape from sharp minima
[1] Z. Xie. A Diffusion Theory For Deep Learning Dynamics: Stochastic Gradient Descent Exponentially Favors Flat Minima. Arxiv: 2002.03495
Practical aspects in training¶
- General procedure
- Techniques for improved convergence and better solutions
Basics: General procedure¶
- If there are not much data - try cross-validation to use all data
- i.e., do splits of train-test, so that all data points are used as test once.
- See Linear Regression module for review.
- Otherwise, do a split of train-valid-test.
- Train: for decreasing the loss
- Valid: for picking the best parameter during training (behave like test in CV)
- Test: Completely unseen in the training process, used to verify the model performance
Basics: Diagnose your loss curve¶
- Linearly decrease: increase the learning rate
- Shaky curves: increase the batch size
- Distant train/valid curves: overfitting
- Overlapping train/valid curves: underfitting
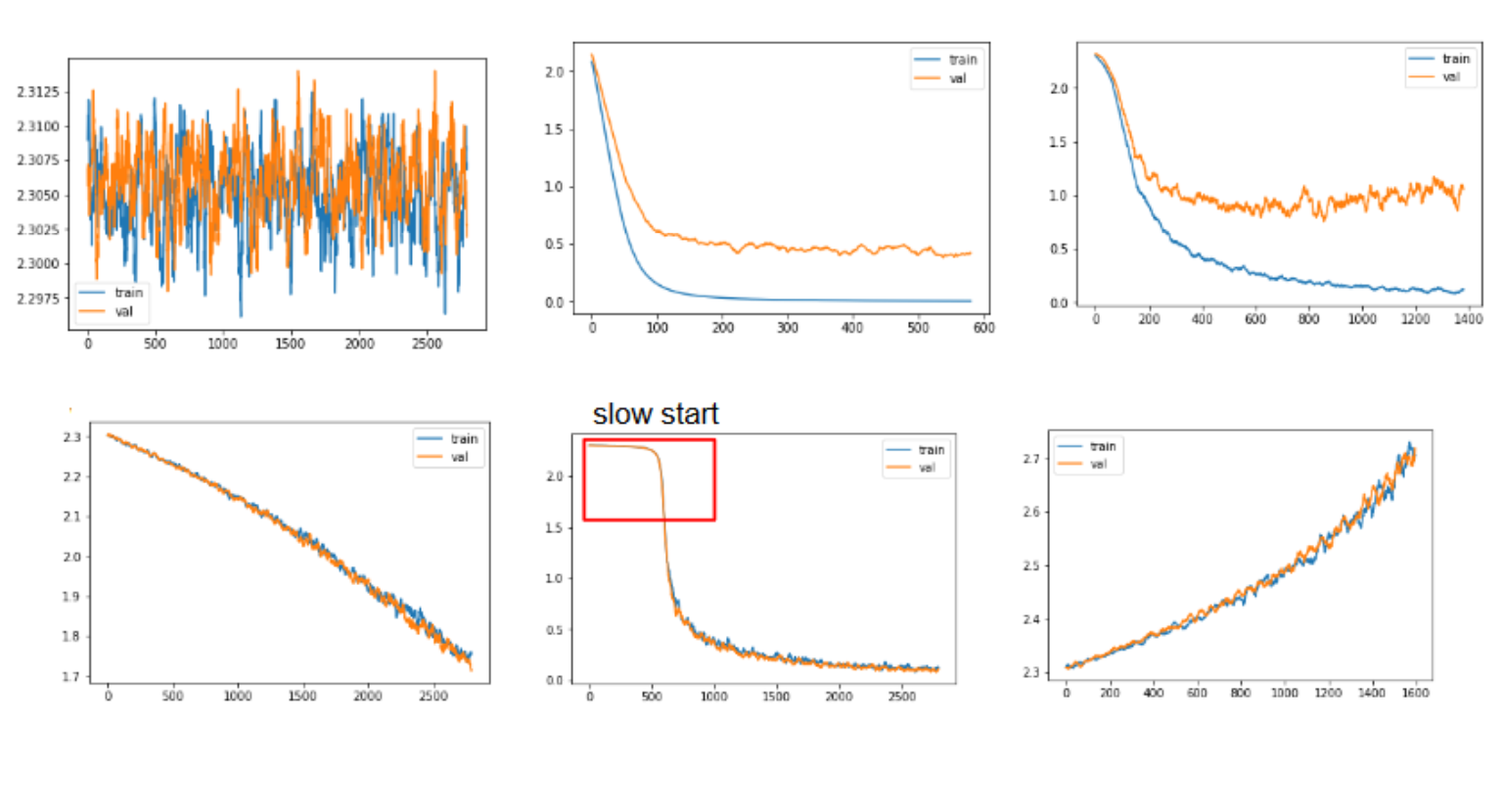
Basics: More on loss curves¶
dev=valid
[1] A. Ng, Nuts and Bolts of Building Applications using Deep Learning, NeurIPS 2016
Intermediate: Caveats and Tuning tricks - I¶
Always normalize and shuffle your data!
- But normalization factors should be based on training dataset only.
Pick the right learning rate: e.g., Grid search [1], or (cyclic) scheduling [2,3]
- Higher learning rate for larger batch size (and larger batch-size if you have a bigger machine)
[1] S. Gugger, How Do You Find A Good Learning Rate
[2] I. Loshchilov, SGDR: Stochastic gradient descent with warm restarts, Arxiv: 1608.03983
[3] L. Smith, Cyclical Learning Rates for Training Neural Networks, 2017
Intermediate: Caveats and Tuning tricks - II¶
Pick the right optimizer: Typically start with Adam, fine-tune with SGD
Start with ReLU or tanh for activation; avoid sigmoid unless for "gate"-like layers
Try overfitting on a small dataset
- If your code/model is correct, the training should converge really fast
Record your training experiments - learn from history
More techniques¶
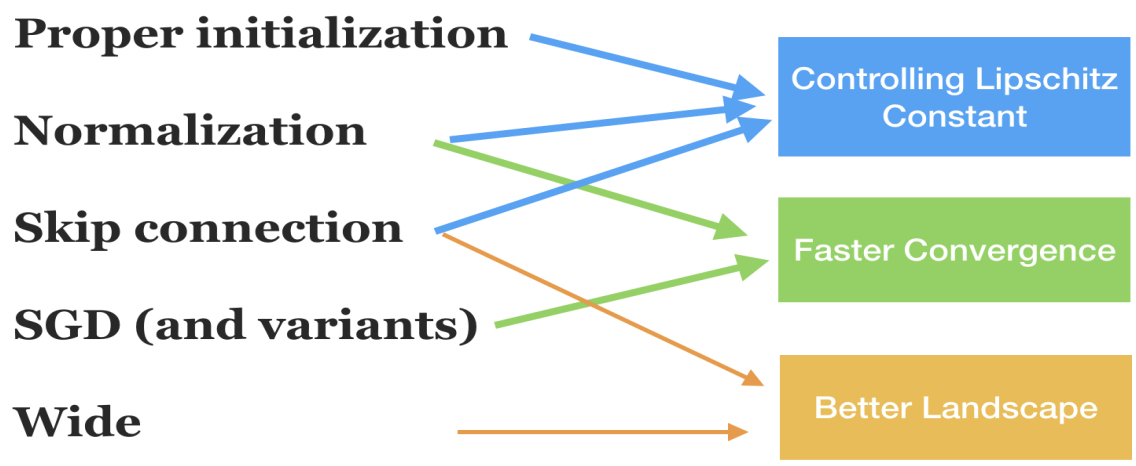
[1] R. Sun. Optimization for deep learning: theory and algorithms. Arxiv 1912.08957 A nice comprehensive summary
More techniques - Weight initialization¶
- Basically to get better initial guesses of the weights [1,2]
- Let $n_i$ be input size, $n_o$ output size, so the weight $W$ of size $(n_i,n_o)$ and let $n=n_i$ or $n=(n_i+n_o)/2$
- Uniform $U[-s,s]$
- Xavier (tanh/sigmoid): $s=\sqrt{3/n}$
- Kaiming (ReLU): $s=\sqrt{6/n}$
- Gaussian $N(0,\sigma^2)$
- Xavier (tanh/sigmoid): $\sigma=\sqrt{1/n}$
- Kaiming (ReLU): $\sigma=\sqrt{2/n}$
[1] X. Glorot, et al. Understanding the difficulty of training deep feedforward neural networks. AISTATS 2010
[2] K. He, et al. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification. 1502.01852
More techniques - Dropout¶
- Randomly "throw away" neurons during training
- so these neuron do not contribute to the prediction and their weights are not updated.
- This is as if multiple NNs are being learned during training
- Avoids overfitting, since now there is a "committee" of NNs
[1] G. Hinton, et al. Improving neural networks by preventing co-adaptation of feature detectors. Arxiv:1207.0580
More techniques - Normalization within Network - I¶
- If we think each NN layer is a small model that we want to fit
- Then it is natural to think about normalizing the "inputs" to these layers
- The inputs, however, are the outputs of the preceeding layer
- Batch Normalization [1] does the trick
- Turns out it maintains the distribution of inputs/outputs of the NN layers
- Leads to faster convergence and perhaps better accuracy

[1] S. Ioffe, et al. Batch normalization: Accelerating deep network training by reducing internal covariate shift. ICML 2015.
More techniques - Normalization within Network - II¶
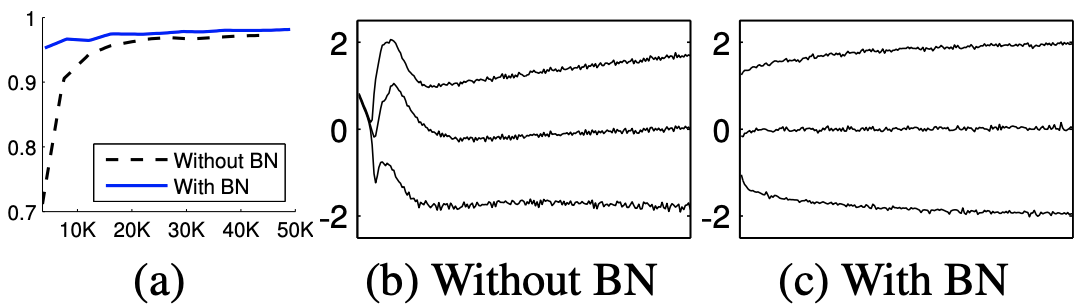
- There are more variants, too, such as weight/layer/instance/group normalization etc.
- See weight normalization [2] for example, it reparametrizes the weights instead of the inputs.
[2] T. Salimans, et al. Weight normalization: A simple reparameterization to accelerate training of deep neural networks. NeurIPS 2016
More techniques - Skip connection¶
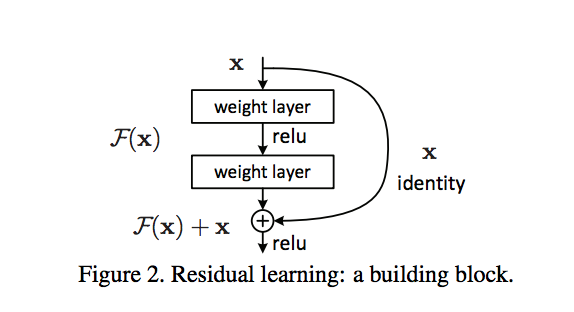
- This is an important type of NN architecture. It improves the convergence and has deeper implications.
- We will come back to this in L17.
Pursuing zero training error?¶
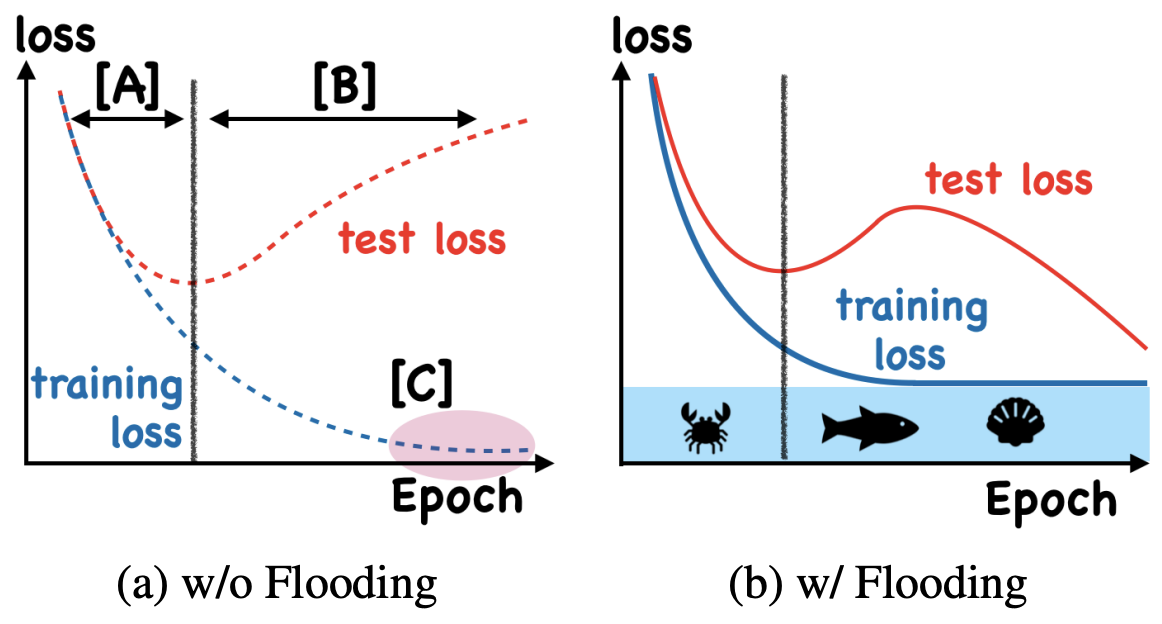
BTW, look at that deep-double descent!
[1] T. Ishida, et al. Do We Need Zero Training Loss After Achieving Zero Training Error? Arxiv: 2002.08709