TODAY: Neural Networks - V¶
- Model calibration
- Adjoint formulation
Motivation¶
All models are wrong, but some are useful.
- In traditional CAE analysis, the physics cannot be precisely captured
- e.g. turbulence closure, constitutive relation modeling
- Uncertainty in prediction/design $\rightarrow$ Large safety factor and performance penalty
- In control and system engineering,
- Non-trivial to design a "clever" and robust controller for the complex and stochastic environment
A machine learning model can be mebedded into the traditional analysis framework, so as to enhance the predictive capability of the latter.
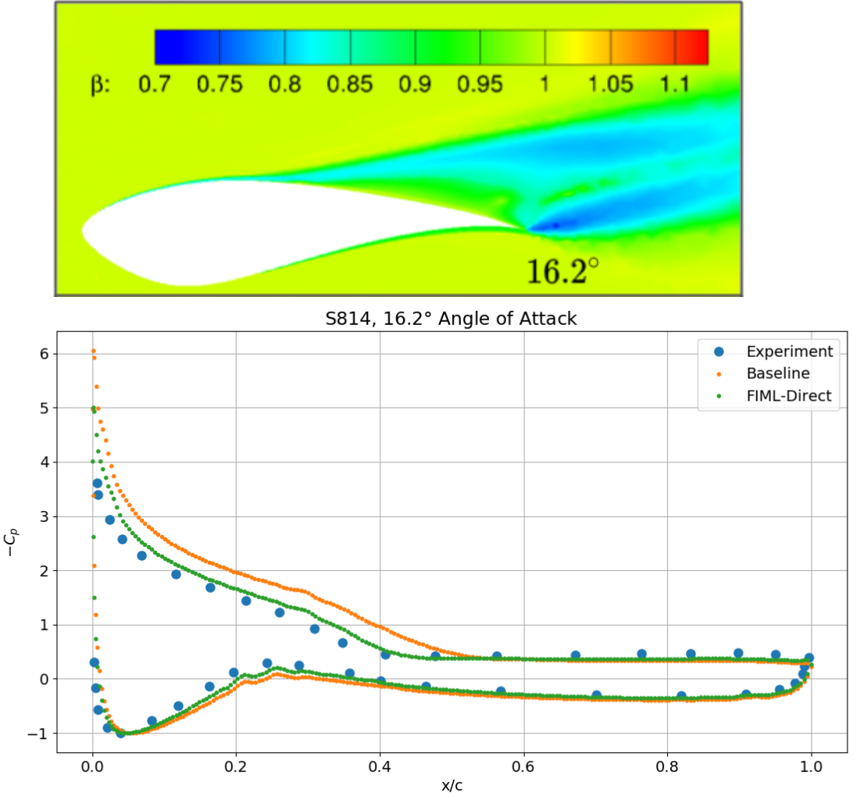(Figure from Holland, Baeder etc. 2019)
Formulation¶
Notations¶
- $\cR(\vu)=0$ represents the governing equation of the problem, and the $\vu$ is state variable. For example,
- Fluid dynamics: $\cR$ - Navier-Stokes equation, $\vu$ - density, momentum, energy
- Solid mechanics: $\cR$ - Force equilibrium, $\vu$ - structural displacement
- System dynamics: $\cR$ - Rigid body motion, $\vu$ - linear & angular displacement/velocity
- $\cJ(\vu)$ is the model error, i.e. the difference between the theoretical model and the reality. For example,
- Fluid dynamics: Surface pressure of an airfoil is extracted from the fluid solution $\vu$ and compared to experimental measurement. The difference in the pressure distribution can be used as $\cJ$.
- Solid mechanics: The deformation of a beam is found from the structural solution $\vu$ and compared to experimental measurement. The difference in the deformation can be used as $\cJ$.
- System dynamics: By a similar idea, the difference in simulation and measured dynamical response.
Calibration model¶
- $\vf=\cM(\vu;\vd)$ represents a machine learning model that is parameterized by $\vf$ and takes in the state variable $\vu$. It returns a set of coefficients $\vd$ to calibrate/correct the model prediction. For example,
- Fluid dynamics: $\vf$ to correct turbulence production term in the RANS equation, so as to improve the pressure prediction.
- Solid mechanics: $\vf$ to correct stress-strain relation, so as to improve the structural deformation prediction.
- System dynamics: $\vf$ to be used as an unknown external forcing term, so as to improve the accuracy of simulation.
- When $\cM$ is incorporated into the analysis framework, the governing equation becomes, $$ \cR(\vu;\vf)=0,\quad \mbox{where } \vf=\cM(\vu;\vd) $$ and similarly, the model error becomes $\cJ(\vu;\vf)$.
Optimization formulation¶
To improve the model, one wants to find the output of the calibration model that minimizes the model error, i.e. $$ \begin{align} \min_{\vf} &\quad \cJ(\vu;\vf) \\ \mathrm{s.t.} &\quad \cR(\vu;\vf) = 0 \end{align} $$
Two strategies to solve the optimization problem,
- Indirect approach:
- First, solve the optimization problem and find the optimal correction factors $\vf$.
- Then, using $\vf$ as training data, fit a calibration model $\vf=\cM(\vu;\vd)$.
- Pros: $\cM$ does not explicitly exist in the governing equation, so easy to implement
- Cons: Size of $\vf$ can be large, so inefficient to train; and accuracy may be sacrificed in model fitting.
- Direct approach:
- Implement the model $\cM$ in $\cR$ and $\cJ$ directly
- Solve a coupled optimization problem that generates the optimal parameters $\vd$ in the calibration model.
The direct approach is solving a slightly different optimization problem, $$ \begin{align} \min_{\vd} &\quad \cJ(\vu;\vd) \\ \mathrm{s.t.} &\quad \cR(\vu;\vd) = 0 \end{align} $$ where $\cJ$ is used the loss function to train the calibration model; the difficulty is the backpropagation of error through the complex governing equation.
Adjoint Method for PDE Constraint¶
Consider the optimization problem in general, $$ \begin{align} \min_{\vtt} &\quad \cJ(\vu;\vtt) \\ \mathrm{s.t.} &\quad \cR(\vu;\vtt) = 0 \end{align} $$ where $\cR(\vu;\vtt) = 0$ is a set of $N$ equations representing the numerical discretization of a PDE. The size of $\vu$ can be way larger than the size of the design variables $\vtt$.
Given the design variables $\vtt^*$, the PDE is usually solved by a certain form of the Newton-Raphson method, $$ \begin{align} \ppf{\cR}{\vu}\Delta\vu^i &= -\cR(\vu^i,\vtt^*) \\ \vu^{i+1} &= \vu^i + \Delta\vu^i \end{align} $$ where the first equation is typically solved using an iterative method.
Formulation by adjoint variables¶
For optimization, one wants the full derivative of $\cJ(\vu;\vtt)$ w.r.t. $\vtt$, i.e. $$ \ddf{\cJ(\vu;\vtt)}{\vtt} = \ppf{\cJ}{\vu}\ppf{\vu}{\vtt} + \ppf{\cJ}{\vtt} $$ where $\ppf{\vu}{\vtt}$ is non-trivial to compute.
From the constraint, one knows, $$ \ddf{\cR(\vu;\vtt)}{\vtt} = \ppf{\cR}{\vu}\ppf{\vu}{\vtt} + \ppf{\cR}{\vtt} = 0 $$ or $$ \ppf{\vu}{\vtt} = \left(-\ppf{\cR}{\vu}\right)^{-1}\ppf{\cR}{\vtt} $$
Therefore, $$ \ddf{\cJ(\vu;\vtt)}{\vtt} = \ppf{\cJ}{\vu}\left(-\ppf{\cR}{\vu}\right)^{-1}\ppf{\cR}{\vtt} + \ppf{\cJ}{\vtt} $$
Now let $$ \vtf^T = -\ppf{\cJ}{\vu}\left(\ppf{\cR}{\vu}\right)^{-1} $$ or $$ \left(\ppf{\cR}{\vu}\right)^T\vtf = -\left(\ppf{\cJ}{\vu}\right)^T $$
This last equation is called the Adjoint Equation, and $\vtf$ is called the Adjoint Variable.
As a result, the full derivate of $\cJ(\vu;\vtt)$ w.r.t. $\vtt$ is computed as follows,
- Given $\vtt$, solve $\cR(\vu;\vtt)=0$ to find $\vu$
- In this process one obtains $\ppf{\cR}{\vu}$.
- Given $\vtt$ and $\vu$, find $\ppf{\cJ}{\vu}$, $\ppf{\cJ}{\vtt}$, and $\ppf{\cR}{\vtt}$.
- Solve the adjoint equation and find $\vtf$. $$ \left(\ppf{\cR}{\vu}\right)^T\vtf = -\left(\ppf{\cJ}{\vu}\right)^T $$
- The gradient of $\cJ$ $$ \ddf{\cJ(\vu;\vtt)}{\vtt} = \vtf^T\ppf{\cR}{\vtt} + \ppf{\cJ}{\vtt} $$
Formulation by Lagrange multipliers¶
Introduce a vector of Lagrange multipliers $\vtf$ $$ \cL(\vu;\vtt) = \cJ(\vu;\vtt) + \vtf^T \cR(\vu;\vtt) $$
Now one wants the full derivative of $\cL(\vu;\vtt)$ w.r.t. $\vtt$, i.e. $$ \ddf{\cL(\vu;\vtt)}{\vtt} = \ppf{\cJ}{\vu}\ppf{\vu}{\vtt} + \ppf{\cJ}{\vtt} + \vtf^T\left( \ppf{\cR}{\vu}\ppf{\vu}{\vtt} + \ppf{\cR}{\vtt} \right) $$
The RHS is $$ \ppf{\cJ}{\vtt} + \vtf^T\ppf{\cR}{\vtt} + \left(\ppf{\cJ}{\vu} + \vtf^T\ppf{\cR}{\vu}\right)\ppf{\vu}{\vtt} $$
One can eliminate $\ppf{\vu}{\vtt}$ by setting the bracket to zero, $$ \ppf{\cJ}{\vu} + \vtf^T\ppf{\cR}{\vu} = 0 $$ or the adjoint equation $$ \left(\ppf{\cR}{\vu}\right)^T\vtf = -\left(\ppf{\cJ}{\vu}\right)^T $$
Extra: Multiple PDE constraints¶
When a multi-physics problem is considered, which is not uncommon in the field of engineering, the optimization problem becomes $$ \begin{align} \min_{\vtt} &\quad \cJ(\vU;\vtt) \\ \mathrm{s.t.} &\quad \cR_j(\vU;\vtt) = 0,\quad j=1,\cdots,m \end{align} $$ where $m$ PDE's are involved, with unknowns $\vU=\{\vu_1,\cdots,\vu_m\}$.
Introduce a set of Lagrange multipliers, or the adjoint variables, $$ \cL(\vU;\vtt) = \cJ(\vU;\vtt) + \sum_{j=1}^m \vtf_j^T \cR_j(\vU;\vtt) $$
Take the full derivative, $$ \begin{align} \ddf{\cL(\vu;\vtt)}{\vtt} &= \ppf{\cJ}{\vU}\ppf{\vU}{\vtt} + \ppf{\cJ}{\vtt} + \sum_{j=1}^m \vtf_j^T\left( \ppf{\cR_j}{\vU}\ppf{\vU}{\vtt} + \ppf{\cR_j}{\vtt} \right) \\ &= \ppf{\cJ}{\vtt} + \sum_{j=1}^m \vtf_j^T\ppf{\cR_j}{\vtt} + \sum_{j=1}^m \left(\vtf_j^T\ppf{\cR_j}{\vU} + \ppf{\cJ}{\vU}\right)\ppf{\vU}{\vtt} \end{align} $$
A set of $m$ coupled adjoint equations is identified as $$ \sum_{j=1}^m \left(\ppf{\cR_j}{\vu_i}\right)^T\vtf_j = \left(\ppf{\cJ}{\vu_i}\right)^T,\quad i=1,\cdots,m $$
Back to Model Calibration¶
- The adjoint method can be readily applied to the indirect approach by letting $\vtt=\vf$.
- Slightly more involved for the direct approach, where $\vtt=\vd$:
$$
\ppf{\cR}{\vtt} = \ppf{\cR}{\vf}\ppf{\vf}{\vd}
$$
- $\ppf{\cR}{\vf}$: Same term in indirect approach.
- $\ppf{\vf}{\vd}$: A new term found by backpropagation of $\cM$