AERSP 597 - Machine Learning in Aerosapce Engineering

Lecture 9, Gaussian Process Regression: Basic concepts

Instructor: Daning Huang

TODAY: Gaussian Process Regression - I

• Historical background: kriging
• Multivariate correlation

References

• GPML Chps. 1, 2, 4
• DACE Toolbox Manual

"Kriging" model by Danie G. Krige

Danie Gerhardus Krige (26 August 1919 – 3 March 2013), South African statistician and mining engineer who pioneered the field of geostatistics. Inventor of kriging.

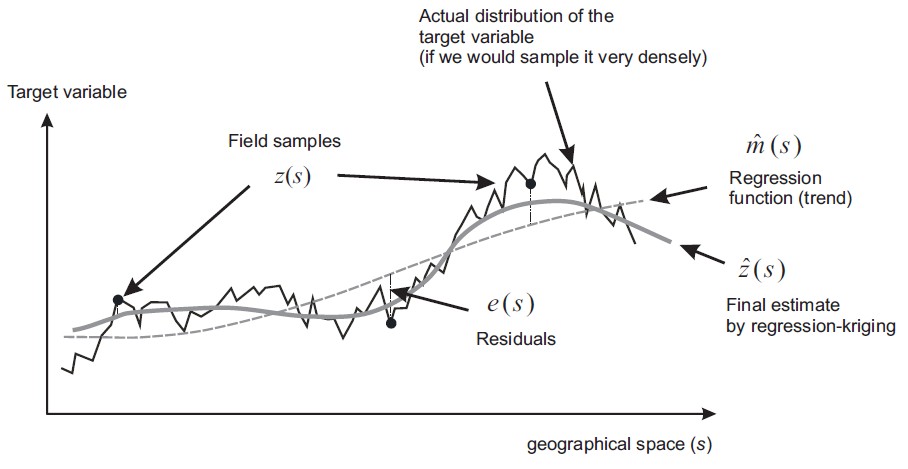
$$ y=\underbrace{f(x)}_{Trend}+\underbrace{e(x)}_{Noise} $$

• Capture the global trend of a dataset, such that the error behaves like white noise.
• But now the noise is location-depedent.

Correlation and Covariance

Covariance function

# Spatial correlation between Gaussian samples at different locations
a = [0.0, 0.0]
x, RV, KS = genGP(5,     # Number of sampling points
                  0.05,  # Length scale in a SE correlation term
                  a,     # Coefficients of second-order polynomial
                  1000)  # Number of GP realizations
plt.figure()
plt.imshow(KS)
plt.colorbar()
_=pltCorr(x, RV)
_=pltGP(x, RV, a,
        bnd=True,             # Plot error bounds
        smp=True)

# Realizations over a set of sampling points
a = [10.0, 0.0]
x, RV, _ = genGP(200,           # Number of sampling points
                 0.0025,        # Length scale in a SE correlation term
                 a,             # Coefficients of second-order polynomial
                 1000)          # Number of GP realizations
_=pltGP(x, RV, a,
        bnd=True,             # Plot error bounds
        smp=True)             # Highlight three samples and plot the mean